Ok then, we’ll meet tomorrow at 7 am CA time!
I pushed what I have, and shortened the plotting window to just [0,4] fm and things look pretty messed up. Outside that range, things just zoom off to infinity and what we were seeing on the meeting was just spurious oscillation due to numerical instability. In short, the HF solver is still broken lol. A coffee on me to whomever fixes it!
Hi @KyleB, Suhonen’s book - from Nucleons to Nuclei could be a good place to start. It also has some simple examples that one can work out to get the feel for how QRPA works. Do you have anything specific in mind?
Thanks! Nothing really specific, I just want to get a better idea of how it works. Maybe construct an RBM emulator for it…
Hey all and @Simone! I wanted to continue the whatsapp convo here to show something interesting:
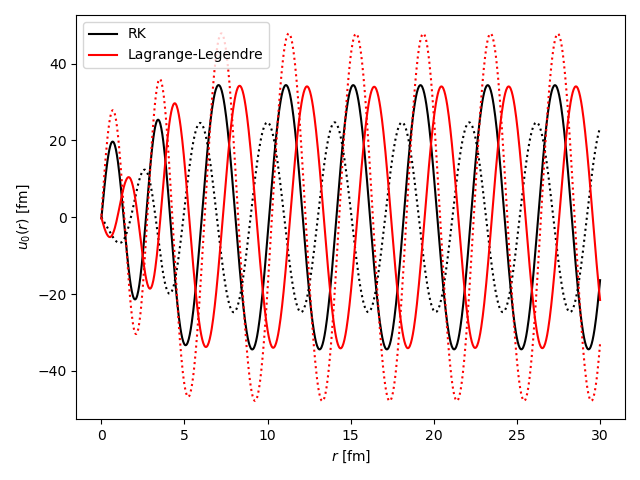
I’ve implemented an R-matrix solver on a Lagrange-Legendre mesh, and am comparing it to RK for single-channel problems. in some cases, the wavefunctions are the same, but in others the disagree. I’m wondering if this has to do with boundary conditions provided to RK. Any thoughts?
Here is the S-wave for scattering on a coulomb + complex Woods-saxon potential:
And here is p-wave:
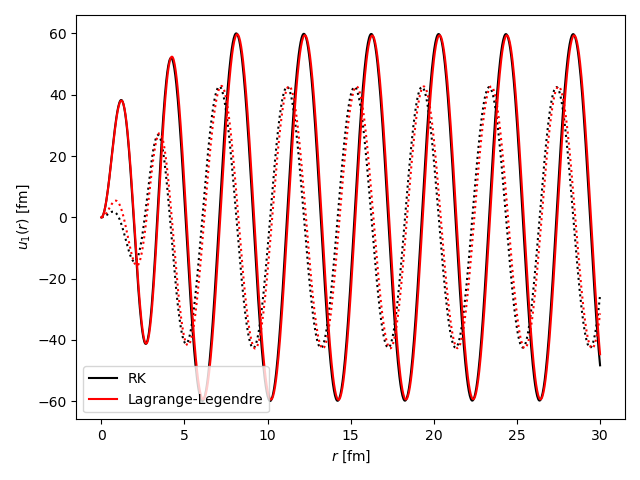
The observables (phase shifts) agree for both cases, but "un"observables (wavefunctions) don’t.
Thank you @KyleB!
In the meanwhile I added another fix to the Runge-Kutta on the repository (the Woods-Saxon was missing the imaginary unit). It’s a simple enough change that I just committed it to your repository without pull request, but please give a look of course.
The R-matrix solver you have is only for single channel, correct?
By the way, it could be nice to get from Fresco or any other trusted solver one extremely simple case to reproduce with our algorithm, just to be confident we have no more bugs.
The investigation on the boundary conditions is indeed interesting, but we already finished the second week out of nominally two weeks. I would propose we just take what we have, good or not, and start trying to apply the RBM.
Hey @Simone , yes I agree, I think we should start constructing an RBM from the RK solver you made.
The R-matrix solver is capable of coupled channels, but I’m not sure if it’s working bc of differences between its wavefunctions and the RK solutions for the single channel case.
Ah, great! In that case, I think it is worth to at least give a look at the R-Matrix implementation, and possibly use it.
You mentioned that there was no difference in the phase shifts in the case you checked, so the difference was just a matter of non-relevant boundary conditions (even in the single-channel RK there is some freedom which brings no physical difference).
At least we are sure the R-matrix will set the boundary conditions we want, while to be honest I should think or ask around about the correct RK boundary conditions for multi-channel.
Are the R-matrix code, and the test you performed recently, accessible?
I just uploaded it to the omp_rbm directory. I still need to do a few things to fix coupled channels, which i will do today.
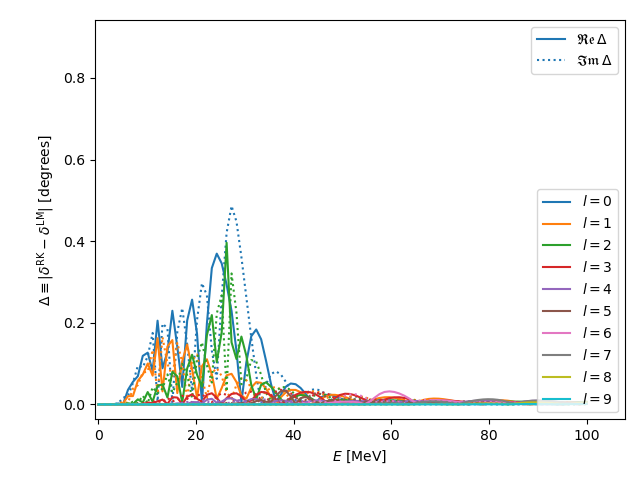
The phase shifts are off by less than a half degree at most between the two solvers, so I’m quite confident the calculation of phase shifts and the solver are working. I doubt an arbitrary phase factor in a training set for RBM will significantly affect the calculation of matrix elements in the reduced basis, but it will be interesting to see.
One other interesting thing about the Lagrange-Legendre mesh is that matrix elements of operators can be calculated in O(N) where N ~30 is the basis size used for the Lagrange mesh. This means that perturbing parameters with non-affine operators can in principle be done quite quickly without doing an approximate affine decomposition (e.g. Empirical Interpolation Method).
Fantastic @KyleB , thanks a lot for your work! This is very interesting.
The new code is too long for me to read throughout, but tomorrow I would like to play around and start thinking about the RBM. If for now we start with the simple version (varying only the 4 depths), if we choose a set of, say, 5 values for each, that’s already 5^4 basis elements. Do you think this sort of numbers can be reasonable? (also @Edgard)
I think this is a great idea!
Per Pablo’s email, it looks like we can ask for an extra week or so on this @Simone. I think that would make sense, if you agree I’ll reply and let him know.
5^4 =625 points in parameter space to train the basis elements = yes, that’s decent.
5^4=625 bases that we will use in total = no, let’s trim that number down by using SVD.
How long does it take to get a data point in parameter space?
Also apologies for being quiet. I had a whole Mexico trip for embassy related purposes planned and the plans fell through so I’ve been dealing with the fallout.
Yes absolutely let’s ask for the extension!
Thanks for clarifying Edgard, and no problem! I did not test that but I suspect it might take more to us to get the code written than to actually calculate 600 points. I am attending an event at the lab until Friday but I hope to manage to get you at least a timeit of one run.
I will plan on spending some time this evening putting in the framework for generating HF training wavefunctions, and will let ya’ll know about timing.
Hi! Sorry for my long silence. I am at a conference right now, I will come back on Monday. But I really hope we can finish this because it is very interesting!
Simone
Hey Simone, agreed, sorry I’ve been MIA as well - I was on vacation the last week and a half. I will sit down today and start generating the training space with the HF solver you implemented.